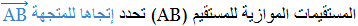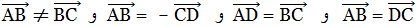المتجهات والإزاحة

I ) تحديد متجهة:
نعتبر النقطتين A وَ B مختلفتين. 

نقول النقطتين A وَ B تحددان كائناً رياضياً يسمى متجهة.

II) إتجاه ومنحى ومنظم المتجهة:
1) الإتجاه:

 

   

2) المنحى:
 



3) المنظم:

 II ) تساوي متجهتين:
تعريف:
نقول عن متجهتين انهما متساويتان اذا كان لهما:

• نفس الاتجاه.
• نفس المنحى.
• نفس المنظم.

ملاحظات:
اذا كان ABCD متوازي الاضلاع، فان:

 
IV) علاقة شال:
خاصية:
كيفما كانت النقط A وَ B وَ C فإن:

 
هذه العلاقة تسمى علاقة شال. 

1) مجموع متجهتين:
خاصية:
مجموع متجهتين هي متجهة. 

 كتابات وتعاريف:
لكل نقطة M من المستوى (P) توجد نقطة وحيدة 'M من المستوى (P) 

 
لكل نقطة 'M من المستوى (P) توجد نقطة وحيدة M من المستوى (P) 

نقول حددنا علاقة من المستوى (P) نحو المستوى (P) 

 
1) صور بعض الاشكال الهندسية بإزاحة:
أ- صورة قطعة: 

 
خاصية:
صورة قطعة هي قطعة تقايسها. 

ب- صورة مستقيم: 

 
خاصية:
صورة مستقيم بإزاحة هي مستقيم يوازيه. 

ملاحظة:

VI ) ضرب متجهة في عدد حقيقي:
تعريف: 

 

 
إذا كانت C نقطة من المستقيم (AB) حيث:

خاصيات:
خاصية 1:

 
خاصية 2: